Сумма внутренних углов выпуклого n-угольника вычисляется по формуле: 180° × (n - 2), где n - количество сторон (углов) многоугольника.
Содержание
Формула суммы углов выпуклого n-угольника
Вывод формулы
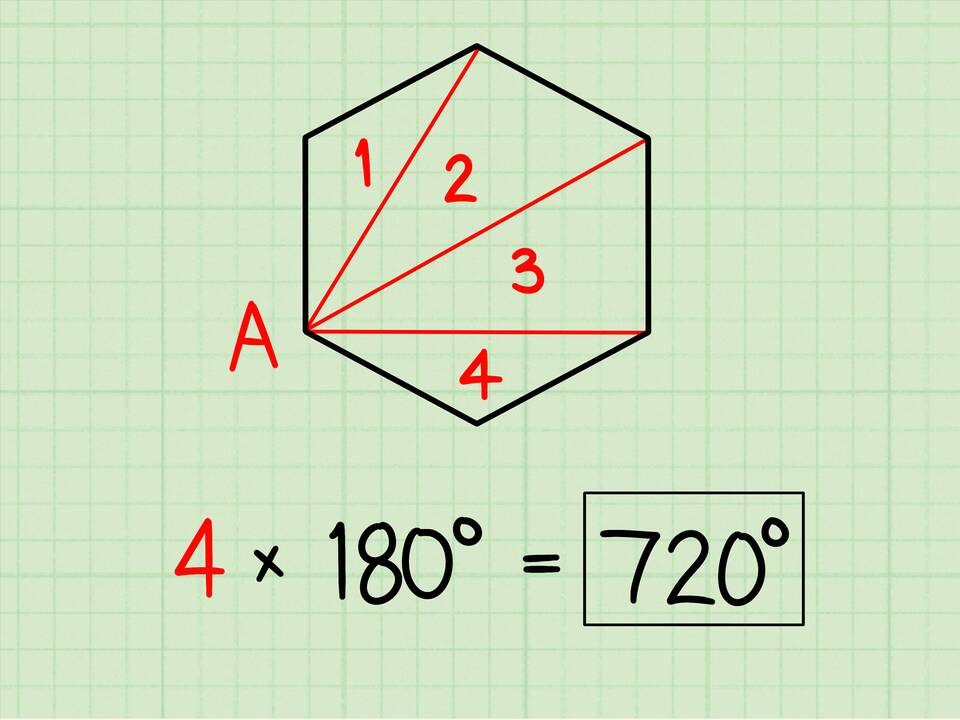
- Из любой вершины n-угольника проведем все возможные диагонали
- Многоугольник разобьется на (n - 2) треугольника
- Сумма углов каждого треугольника равна 180°
- Общая сумма углов многоугольника: 180° × (n - 2)
Примеры расчетов
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | 180° × (3-2) = 180° |
| Четырехугольник | 4 | 180° × (4-2) = 360° |
| Пятиугольник | 5 | 180° × (5-2) = 540° |
| Шестиугольник | 6 | 180° × (6-2) = 720° |
Частные случаи
- Для правильного n-угольника каждый угол равен: [180° × (n - 2)] / n
- Сумма внешних углов любого выпуклого n-угольника всегда равна 360°
Применение формулы
Зная сумму углов n-угольника, можно:
- Находить неизвестные углы в многоугольниках
- Доказывать геометрические теоремы
- Решать задачи на построение
- Определять возможность существования правильных многоугольников
Для невыпуклых многоугольников
Формула 180° × (n - 2) остается верной и для невыпуклых многоугольников, если измерять углы в стандартном направлении (против часовой стрелки).
Графическая иллюстрация
Разбиение n-угольника на треугольники можно представить следующим образом:
- Выбрать одну вершину многоугольника
- Провести диагонали во все несмежные вершины
- Полученные треугольники не будут пересекаться
- Их общее количество всегда будет равно (n - 2)
Историческая справка
Данная формула была известна еще древнегреческим математикам. Евклид в своих "Началах" использовал аналогичный подход для доказательства свойств многоугольников.