Сумма внутренних углов выпуклого n-угольника является важной характеристикой в геометрии, позволяющей решать различные задачи на вычисление углов многоугольников.
Содержание
Сумма внутренних углов выпуклого n-угольника является важной характеристикой в геометрии, позволяющей решать различные задачи на вычисление углов многоугольников.
Формула суммы углов
Для любого выпуклого n-угольника сумма внутренних углов вычисляется по формуле:
S = (n - 2) × 180°
где n - количество сторон (углов) многоугольника.
Примеры вычислений
| Многоугольник | Количество сторон (n) | Сумма углов |
| Треугольник | 3 | (3-2)×180° = 180° |
| Четырехугольник | 4 | (4-2)×180° = 360° |
| Пятиугольник | 5 | (5-2)×180° = 540° |
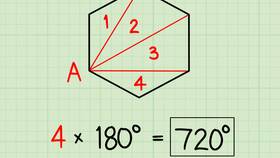
| Шестиугольник | 6 | (6-2)×180° = 720° |
Доказательство формулы
- Выберем произвольную точку внутри n-угольника
- Соединим эту точку со всеми вершинами многоугольника
- Получим n треугольников
- Сумма углов всех треугольников: n × 180°
- Вычитаем 360° (сумма углов при центральной точке)
- Получаем: (n - 2) × 180°
Свойства выпуклых многоугольников
- Все внутренние углы меньше 180°
- Диагонали лежат внутри многоугольника
- Любая сторона многоугольника целиком лежит по одну сторону от прямой, содержащей любую другую сторону
Применение формулы
Зная сумму углов n-угольника, можно:
- Находить неизвестные углы правильных многоугольников
- Решать задачи на построение
- Доказывать геометрические теоремы
- Определять возможность существования многоугольника с заданными углами
